Prologue
I found an excellent unfinished preprint by André Henriques and C.L. Douglas. I suspect Henriques wrote it, though, because it rings of his other writing. It's filled with beautiful diagrams and tables; go have a look at it yourself. This all spilled out of my investigation into what is called the stringor bundle, which plays the same role for string manifolds that the spinor bundle plays for spin manifolds.
Prequel
A huge part of this story has to do with defects; essentially, when one prescribes a string structure to a manifold, many of the defects are eliminated. Ta-da! Except, that's not the whole story. Actually, we need a geometric string structure, and these are actually not easy to come by. In fact, we can actually detect conformal anomalies by finding obstructions to lifting the spin structure to a geometric string structure. So, where do we look for these? A good hunch is at the boundary of a spin manifold M. Since the stringor bundle is defined as a string structure acting on the loop group of M, we can look for twists and kinks at the boundary which would prevent the manifold from being soldered to a frame bundle. A classical example of a frame bundle would be the (co)tangent manifold of M, and the solder form would be written as as a bilinear form 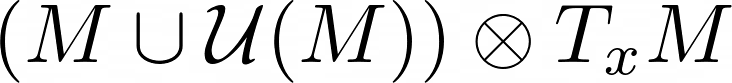
As a sidenote, I feel somewhat queazy about using the curly U notation here, because in a recent preprint I actually used this notation to refer to somesort of universal lightcone, rest assured that this is in fact the standard notation (at least in classical topology) for a neighborhood.
So anyways, Parker Emmerson, a great but kind of wacky (that's how I like 'em!) independent mathematician has been getting really into string theory. I kind of misinterpreted/confused his work on "Morse energy" with his work on strings, and long story short, I began talking about Morse strings, which are 3-connected wormhole-like strands which connect black holes (and other Hawking-Penrose Points) to "exchange partners." That is to say, the notion of infalling particles entering black holes being entangled with outgoing particles, becomes a little perverted: rather than a simple monogamous entanglement between particles, it is actually a foursome consisting of the particles themselves, the black hole, and some distant massive body which are caught in a love diamond. The Morse string, then, is the line of communication between the black hole and its partner, and the particles are merely unwitting accomplices.
Think of this like one giant Manhattan project, where none of the particles are told about the true nature or purpose of their activities, but simply go about minding their own business. Behind the scenes, we have some giant Diracesque cosmic string coupling the Shannon entropy of the two massive bodies, enabling the evolution of the cosmos.
Return to Grace
Now, what does this have to do with defects? Well, in principle, since stringors are like spinors which act on 3-connected spaces, then the physical picture is that an anomaly is an infinitely tense bit of a Morse string. Essentially, all of the supersymmetric affairs are blocked by this kink in the information glide plane. Think of these kinks as cavities in a Frobenius algebra. The classical "Pants diagram" does not have these holes, and are open-ended; however, imagine a different type of cobordism, where two pairs of pants are sewn together at the feet. Then, we have a hole between the legs. This sounds crazy, I know, but please humor me. Imagine that this hole is a special physical object that quarks (anything with a color charge) cannot enter. Then, we have free-flowing exchange particles (massless bosons) which are the only bits of matter capable of occupying this space.
Charm quarks have recently been found inside protons, which is very bizarre, because charm quarks actually weigh MORE than the proton itself! This only makes sense with QM: we have to treat the Frechét space of the charm quark as existing inside the probability (Frechét) space of the proton; when we average out, the small subset of the proton's probability space that we call a charm quark is normalized, alongside all of the other data, to one, and so it evens out. However, this is unsatisfying unphysical. I believe that this Frobenius hole, this Morse string kink, can explain what is really going on under the hood. I am not sure exactly how to formalize this yet, but there are a few different possibilities: perhaps the proton contains holes in the bulk which causes the charm meson to wrap around its boundary. We would have to imagine that some time-step operator, which distorts the entropy of the quark, would deflect some of the energy, causing the proton to become "work-locked." In this scenario, the proton becomes essentially rigid during the periods where the charm quark "occupies" (hugs) it, and acts elastically (relativistically) at all other moments.
Or (humor me again), what if there are antiphotons, and the interactions between the photons and antiphotons that occur inside the proton free it from the presence of charm? Just a hunch.